[MITx: 6.00.1x] Introduction to Computer Science and Programming Using Python (Week 6)

สำหรับ Blog ในตอนนี้ จากที่เรียนมาทั้งหมด พวกว่าทุกคนอยากให้ Code ที่เขียนขึ้นมามีแนวคิดการทำงานต่างกัน หรือที่มีคำเท่ห์ที่เรียกว่า Algorithm ส่วนทำได้มีประสิทธิผล( Performance) และถูกต้อง แล้วอะไรที่บอกว่าเร็วหละ ตอนนี้เน้นส่วนเรื่องที่บอกว่าเร็ว Performance ดี เรามองได้ใน 2 มุมมอง

  • Time - เวลา
  • Space - พื้นที่ของหน่วยความจำที่ใช้

การมาวัดมันมีหลายแบบ เช่น จับเวลา, นับ Operation ที่ใช้ หรือแม้แต่การดูพื้นที่ที่ใช้ไป แต่มันมีปัญหาจุกจิกมากมาย ทั้งที่เรื่องจำนวนข้อมูลนำเข้า(Data Set) และ Enviroment(เช่น พวก Hardware ต่างๆ) ในทาง Computer Science ก็เลยมี Idea ในการวัดอีกแบบ คือ Abstract Notation Order of Growth ครับ

Abstract Notation Order of Growth คือ อะไร

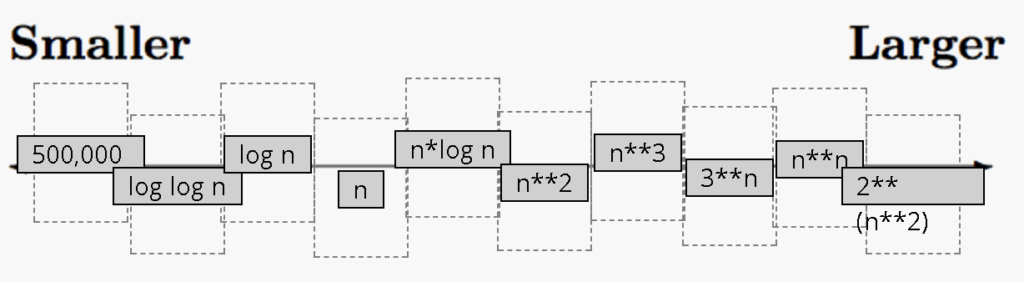
  • แล้วเรามองมุมไหนดีหละ
    • ดีที่สุด
    • กลาง
    • แย่ที่สุด - เราใช้ Big O มาแทนครับ
  • ปกติ เราสนใจเคสที่แย่ที่สุดครับ โดยตัว Order of Growth สามารถแบ่งเป็นกลุ่มๆได้ ดังนี้
  • เราตีความ Algorithm โดยใช้วิธีการที่เป็นมาตรฐาน โดยมีหลักการนับ ดังนี้
    • นับ 1 สำหรับ Operation ต่างๆ  O(1)
      def program1(x):
    #Code ในส่วนนี้มี 1 Operation คือ = โดยยัดค่า 0 ลงไป
    total = 0
    • ถ้ามีเงื่อนไขหละ โดย เราต้องคิดแยก Case ฺBest Case และ Worst Case ด้วย
      def program3(L):
    #Do something

    if highestFound == None:    #--------- O(1) 
        highestFound = x        #--------- O(1) 
    elif x > highestFound:      #--------- O(1) 
        highestFound = x        #--------- O(1) 

    #สรุปจาก Code ชุดนี้
    #>> Best Case = 2 (เข้า If แรกแล้วเป็นจริงเลย)
    #>> Worst Case = 4 (เข้า If แรก + If ชุดที่ 2)
    • ถ้า Code มีการทำซ้ำพวก For / While ให้นับเป็น n ครั้ง O(n)
      def program1(x):
    #Do something

    #ใน Code ส่วนนี้มีการทำซ้ำ n ครั้ง โดย n=1,000
    #ใน for มีการ Check เงื่อนไขนับเป็น O(1)--------------[1]
    for i in range(1000):
        #คำส่ังบรรทัดนี้ มี 2 Operation O(2)--------------[2]
        #หากลองเขียน Code อีกแบบ ได้เป็น x = x + 1
        total += i
    
    #สรุปรวมสำหรับใน Code ส่วนนี้เอา [1] + [2] ได้ค่าเป็น O(3)
    #และ Code ส่วนนี้มีการทำงานทั้งหมด 1000 ครั้ง 
    #Big O สำหรับ Code ในส่วนนี้ คือ 3 * 1000
    • Note: สำหรับในเคส Loop ที่มีเงื่อนไขมาเกี่ยวข้อง เราต้องคิดแยก Case ฺBest Case และ Worst Case
    • Law of Addition - ถ้า Code มีการทำงานที่ต่อเนื่องกัน ให้เอาแต่ละส่วนมาบวกกัน
    • Law of Multiplication - ถ้า Code มีการทำงานที่ซ้อนกัน ให้เอามาคูณกัน
    • TIP: การดู Order of Growth เราไม่สามารถมองจุดเดียวแล้วบอกได้เลย เราต้องไล่การทำของ Code ในสาย Software  Engineering เรียกว่า Control Flow จากนั้นจึงค่อยมาจาก Best Case และ Worst Case ของโปรแกรม
    • ตอนนี้จาก Code ของเราคงได้สมการมาชุดนึง แล้วที่นี้ดูยังไงว่าเป็น Worst Case หละ การดูนั้นง่ายมากเลย โดยดู Dominant terms เอาพจน์ที่ใหญ่ที่สุดมาอ้างถึงครับ
  • ตัวอย่างการคำนวณของ Fibonacci
    • แบบที่ 1 - ใช้ Loop โดย ฺBest Case = O(1) และ Worst Case = O(n)
      def fib_iter(n):
   if n == 0:
      return 0
   elif n == 1:
      return 1
   else:
      fib_i = 0
      fib_ii = 1
      for i in range(n-1):
         tmp = fib_i
         fib_i = fib_ii
         fib_ii = tmp + fib_ii
      return fib_ii
    • แบบที่ 2 - ใช้ Recursive โดย ฺBest Case = O(1) และ Worst Case = O(2n)
      def fib_recur(n):
   """ assumes n an int >= 0 """
   if n == 0:
      return 0
   elif n == 1:
      return 1
   else:
      return fib_recur(n-1) + fib_recur(n-2)
      • สำหรับในแบบ Recursive Worst Case = O(2n) ลองดูจาก Recursion Tree ได้เลยครับ
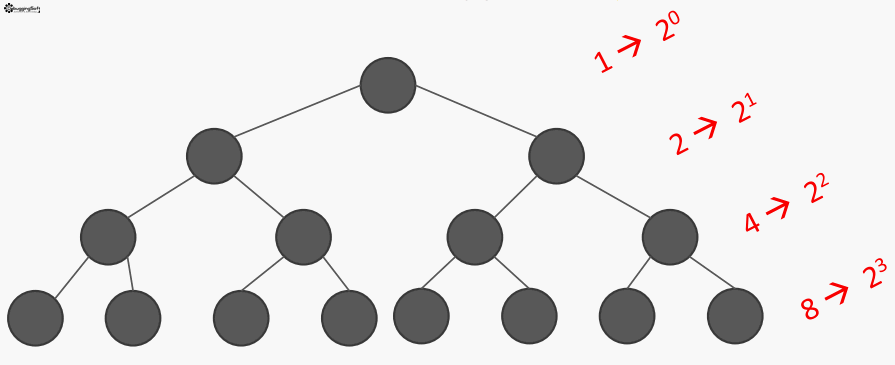
    • Note: เห็นว่าแต่ละวิธี Big O แตกต่างกันมาก แต่เราต้องเลือกใช้ให้เหมาะสมกับงานครับ
  • สรุปหลังจากรู้วิธีการคิดแล้ว มาทวนอีกรอบ
    ComplexityRunning timeExample
    O(1)constantงานที่มีลักษณะทั่วๆไป
    O(log n)logarithmicงานที่มีลักษณะ Divide & Conquere
    O(n)linearงานที่มีลักษณะทำซ้ำ
    O(n log n)log-linearงานที่มีลักษณะทำซ้ำ และมีการลดทอนข้อมูล เช่น Bisection Search
    O(nc)polynomialงานที่มีลักษณะทำซ้ำ ซ้อนกัน เช่น Code ที่มี Loop for ซ้อนกัน (Nested)
    O(cn)exponentialส่วนใหญ่เป็นงานที่มีลักษณะของ Recursion

Search & Sort คู่แท้เรื่องอัลกอริทึม

  • ถ้าใครเคยเรียนมาตอนปริญญาตรี พบว่าเรื่อง Search กับ Sort 2S นี้ มันคู่กับการวัดประสิทธิภาพ ใน Class นี้เหมือนกันครับ แต่ก็มีบางเรื่องแปลกใหม่เหมือนกันนะ แต่ผมคงไม่ลงลึกการคิด Big O นะครับ มันออกแนวตัวอย่างของการคิดในเรื่องที่แล้วมากกว่า
  • Search

    This slideshow requires JavaScript.

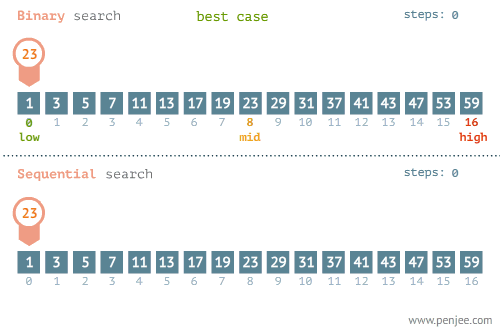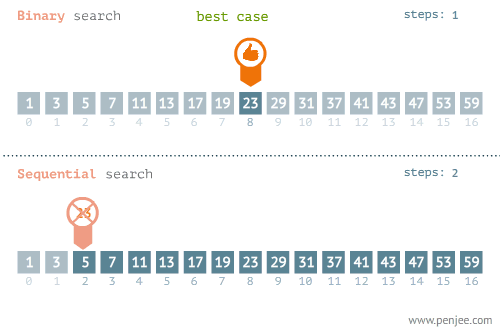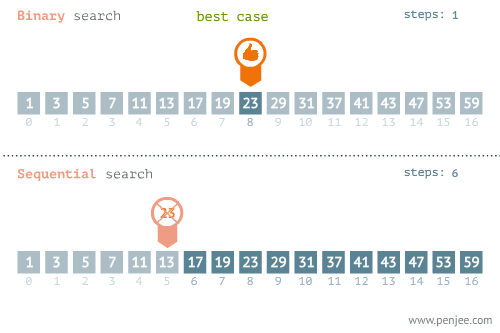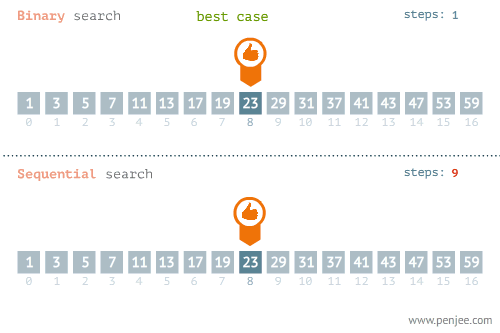
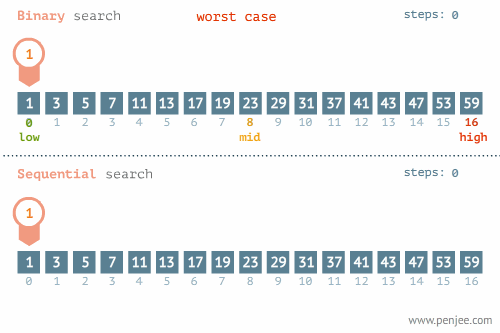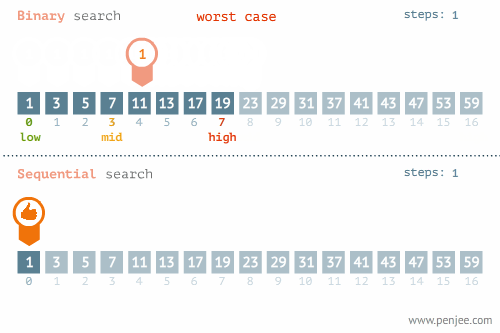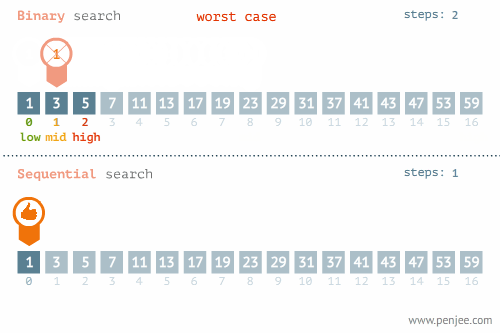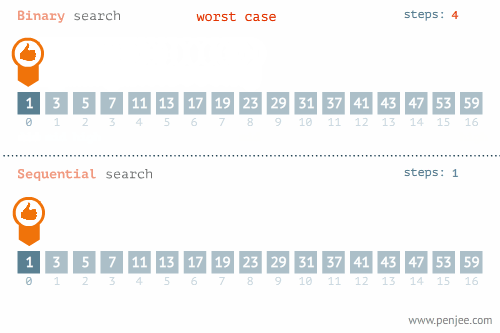
    • Linear Search - O(n) อาจจะมองว่าเป็นการ Bruted Force ค่อยไล่ถามไปทีละตัวจนกว่าจะเจอ
    • Binary Search - O(log n) ใช้แนวคิด Divide & Conquer แต่ข้อมูลต้องเรียงลำดับมาแล้ว
  • Sort

    • Bogo Sort - คาดการณ์ไม่ได้ เพราะเป็นการเรียงแบบสุ่ม ไม่มีกฏเกณฑ์ที่ชัดเจน หากคำนวณมันเป็นเรียงสลับเปลี่ยนตำแหน่งที่เป็นไปได้ของข้อมูลทั้งหมด
    • ฺBubble Sort - O(n2)
    • Selection Sort - O(n2) เร็วกว่า Bubble Sort เพราะ Step ย่อยในการสลับข้อมูลน้อยกว่า ใน Loop 1 รอบมีการสลับข้อมูล 1 ครั้งเท่านั้น
    • Merge Sort - O(n log(n)) เร็วที่สุด เพราะใช้แนวคิด Divide & Conquer แบ่งข้อมูลจากนั้น Sort ในหน่วยที่เล็กที่สุด
  • Amortized Cost
    • ผมมองว่าเรื่องนี้เป็นการจัดการเรื่องลำดับของการประมวลผลมากกว่า มันต้องดูกับงานที่ใช้ด้วย เช่น ถ้ามีการ Search บ่อยๆ ในข้อมูลชุดเดียวกัน ถ้า Sort ก่อนแล้วใช้ Binary Search มันช่วยลด Cost ด้านเวลาที่ใช้ในการค้นหาได้ ถ้าเรามีการเรียงข้อมูลก่อน
    • ถ้าผมจำไม่ผิดพวก ETL บางเจ้ามี Step ให้ Sort แล้วถึงสามารถจัดการกับข้อมูลต่อได้

Reference

 

Discover more from naiwaen@DebuggingSoft

Subscribe to get the latest posts sent to your email.

Tags

Related Posts